Résumé

La reconstruction énergétique dans le calorimètre ATLAS consiste à associer les dépôts d’énergie des particules dans le calorimètre avec la particule qui les a causés. C’est une étape cruciale pour identifier les particules et reconstruire l’événement qui les a produites. Les méthodes actuelles de reconstruction reposent sur des algorithmes dont la complexité croît de manière quadratique, ce qui pose un défi pour la mise à niveau du LHC haute luminosité (HL-LHC), qui promet une augmentation significative du nombre de collisions par événement et, par conséquent, de la complexité de chaque événement. Travaillant sous la direction du Dr Max Swiatlowski, j’applique PointNet et d’autres approches d’apprentissage automatique à la reconstruction énergétique dans le calorimètre ATLAS.

Cet été, j’ai eu la chance de recevoir le prix Erich Vogt First Year Summer Research Experience Award (FYSRE), me donnant l’opportunité de travailler à TRIUMF, le centre canadien d’accélération des particules.

Notez que ce résumé de mon premier mois de travail est destiné à un public semi-technique. Si vous avez des questions sur les détails ou sur l’un des termes que j’utilise, n’hésitez pas à me contacter.

Comprendre le Problème

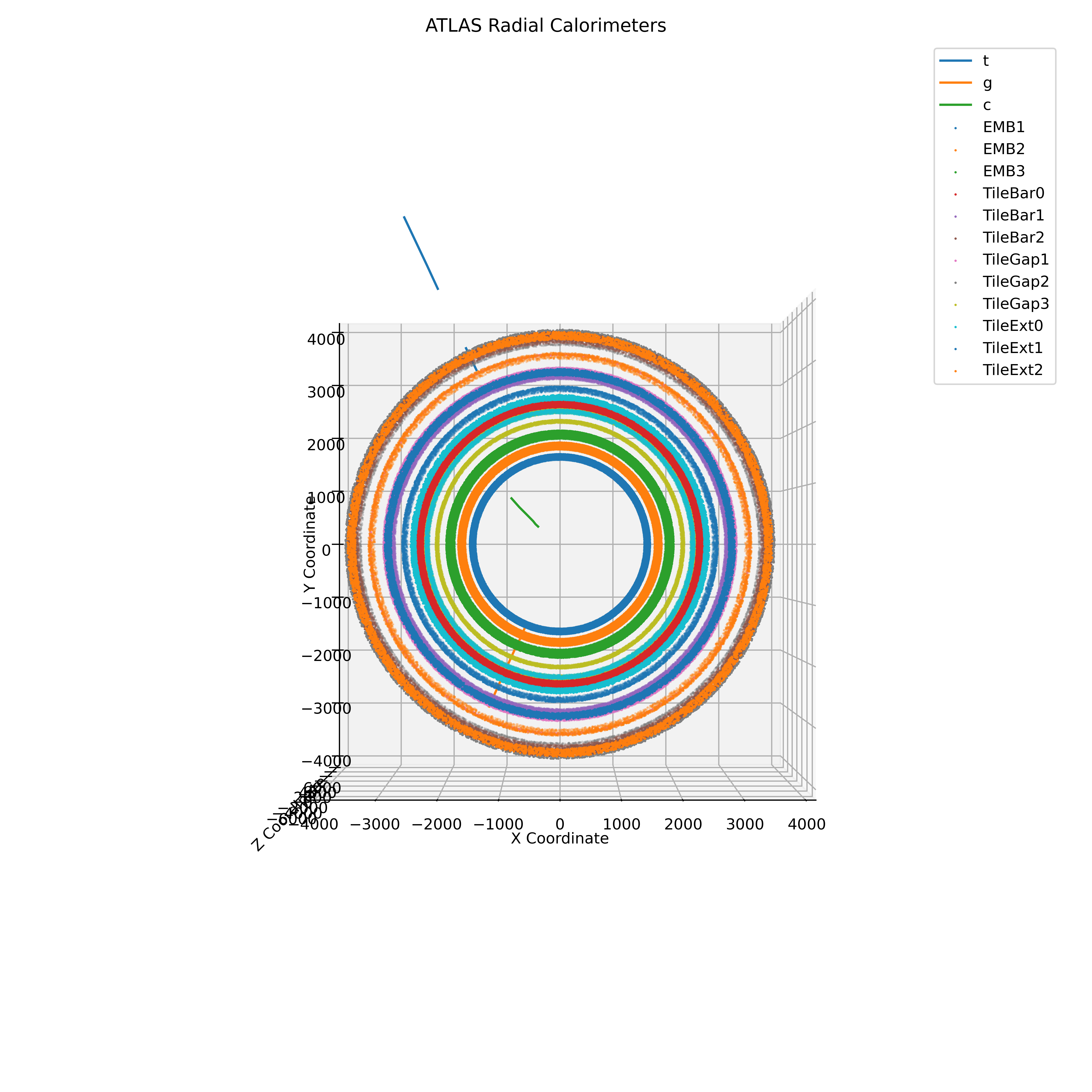
Il existe deux types principaux de détecteurs présents dans ATLAS. D’abord, les traceurs internes utilisent des détecteurs en silicium pour mesurer la trajectoire des particules chargées. Grâce au champ magnétique du LHC, la courbure de la trajectoire des particules peut être utilisée pour déterminer la quantité de mouvement des particules dans le traceur; cependant, pas leur énergie. Après avoir traversé le traceur interne, les particules entrent dans le deuxième type de détecteur, le calorimètre. Le calorimètre ATLAS est composé de nombreuses couches, incluant à la fois les calorimètres électromagnétiques et hadroniques, qui peuvent absorber et lire l’énergie de (la plupart) des particules qui les traversent.

L’une des difficultés du calorimètre ATLAS est que relier les dépôts d’énergie dans les couches du calorimètre aux traces dans le détecteur interne n’est pas trivial pour plusieurs raisons.

Certaines particules ne laissent pas de traces dans le traceur interne, comme les photons et les hadrons neutres, qui n’ioniseront pas les détecteurs en silicium.
Certaines particules laisseront des traces dans le traceur interne mais pas dans le calorimètre, comme les muons, qui sont si massifs qu’ils traversent le calorimètre sans interagir avec lui.
Enfin, et surtout, comme le LHC fait entrer en collision des paquets contenant des millions de protons, il y a souvent de multiples trajectoires de particules très rapprochées. Cet effet, souvent appelé “pileup”, peut rendre la relation entre les impacts dans le calorimètre et les traces dans le détecteur interne très coûteuse en termes de calcul. Avec la mise à niveau du LHC vers le HL-LHC (LHC haute luminosité), le nombre de collisions par événement augmentera considérablement, rendant ce problème encore plus difficile.

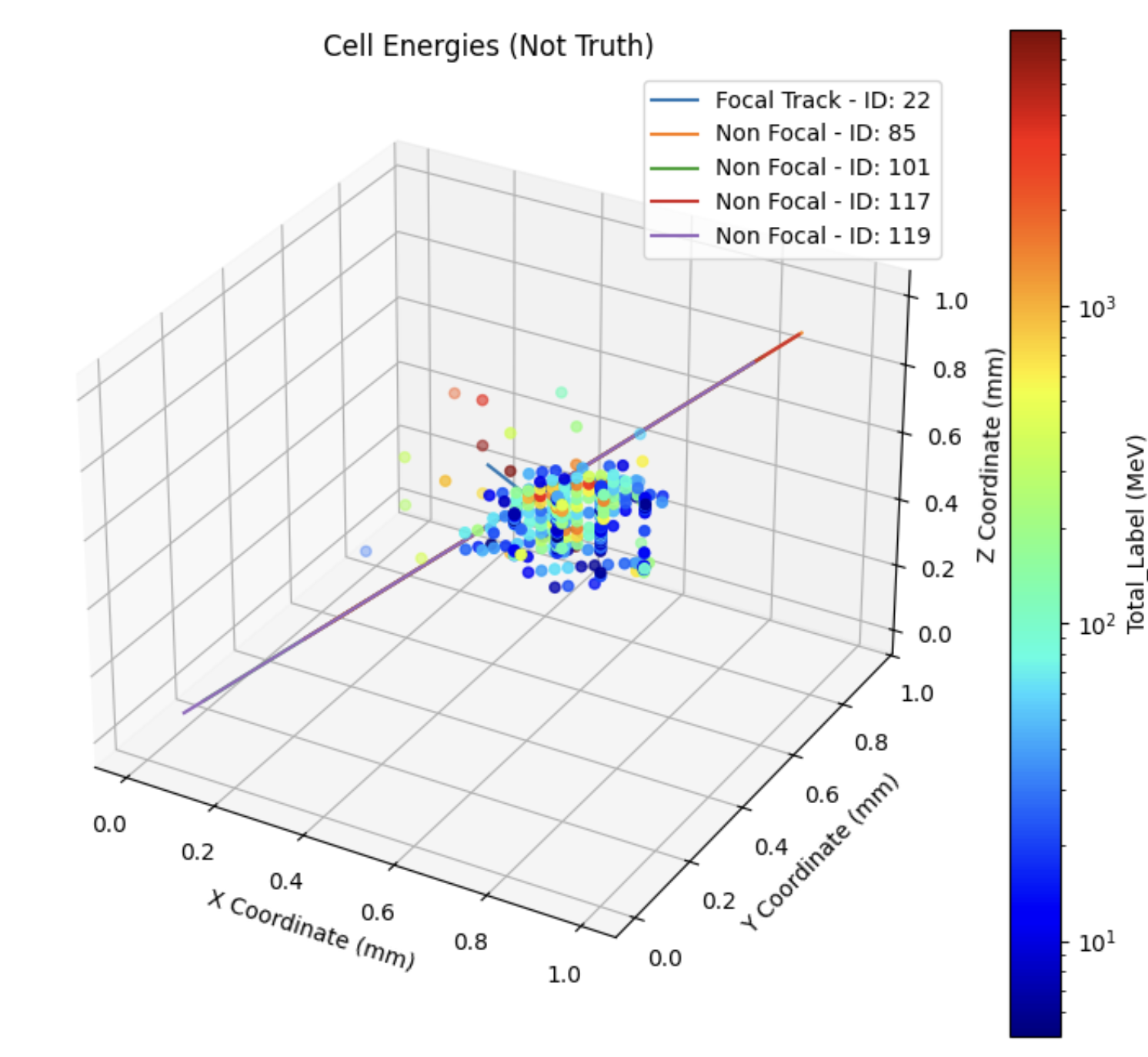
Développer le Modèle

PointNet

Les données sont représentées sous forme de nuage de points où chaque point est un impact dans le calorimètre. En tant que nuage de points sparse, les données ne sont pas bien adaptées aux modèles traditionnels qui reposent sur des entrées de longueur cohérente. Une approche consisterait à placer les points dans une grille 3D ; cependant, cela serait coûteux en termes de calcul et nécessiterait un réseau d’une complexité extrêmement élevée. La solution que nous utilisons pour ce problème est PointNet, un modèle capable de traiter directement les nuages de points sans avoir besoin de les convertir en grille. PointNet a l’avantage de pouvoir traiter des nuages de taille arbitraire ; cependant, il nécessite plusieurs perceptrons multicouches pour fournir l’invariance spatiale et d’ordre attendue d’un réseau neuronal. Cette idée a été introduite pour la première fois dans l’article PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation.

Prétraitement des Données

L’un des plus grands défis de l’adaptation du modèle PointNet au calorimètre ATLAS est de représenter les données de manière significative pour le modèle. Pour ce faire, nous avons besoin de plusieurs entrées catégorielles, y compris des informations sur les traces, des impacts dans le calorimètre et des informations sur les traces non focales. Bien que cette étape puisse sembler triviale, il y a plusieurs considérations de conception concernant les cas limites. Par exemple, certaines traces, lorsqu’elles sont extrapolées au calorimètre, n’intersectent pas avec aucune des couches du calorimètre. Ceci est principalement observé autour de l’eta = ±2,48, où des composants structurels du détecteur empêchent la trace d’intersecter avec le calorimètre. De plus, le modèle ne peut pas traiter l’énorme quantité de données dans un seul événement, donc chaque trace est limitée à un rayon maximum eta-phi (eta-phi est un système de coordonnées dans le calorimètre, analogue à un système theta-phi dans un système de coordonnées sphériques) pour concentrer le modèle sur les cellules les plus pertinentes.

De plus, le temps de traitement des données brutes est significatif, ce qui rend son optimisation une étape cruciale dans le développement d’un modèle pouvant être utilisé en temps réel.

Recherche de l’Espace des Hyperparamètres

En fin de compte, avec un modèle aussi complexe que PointNet, il est important de rechercher l’espace des hyperparamètres pour trouver le modèle optimal. Il a été observé que dans quelques cas, le modèle ne convergerait pas, mais plus important encore, le modèle pourrait connaître un effondrement modal, où le modèle déclarerait tous les impacts comme étant soit du signal, soit du bruit, au lieu de la classification par impact souhaitée. La principale mitigation contre cela, cependant, n’est pas les hyperparamètres mais le prétraitement des données. En particulier, l’extension de l’ensemble d’entraînement a considérablement réduit l’occurrence de l’effondrement modal. L’effondrement modal initial est supposé être une conséquence de notre entraînement initial sur seulement 2000 événements (~125000 traces) avec plus de 5 millions de paramètres entraînables. Une hypothèse sur la raison pour laquelle cet effondrement modal était si répandu est son efficacité pure à réduire la fonction de perte. Avec un modèle parfait connaissant ce comportement tout-ou-rien, la précision pourrait être aussi élevée que 87 %. Bien que techniquement intéressant, ce modèle est inefficace car il ne nous permet pas de faire des prédictions à partir des sorties du modèle au-delà de ce qui est déjà possible en appliquant un simple cut pt (momentum).

Pour une recherche d’hyperparamètres, au-delà de la formation des données d’entraînement et de la taille du modèle, nous avons complété un balayage de l’espace de phase pour le taux d’apprentissage, le nombre d’époques et la pondération de l’énergie de la fonction de perte en utilisant Weights and Biases.

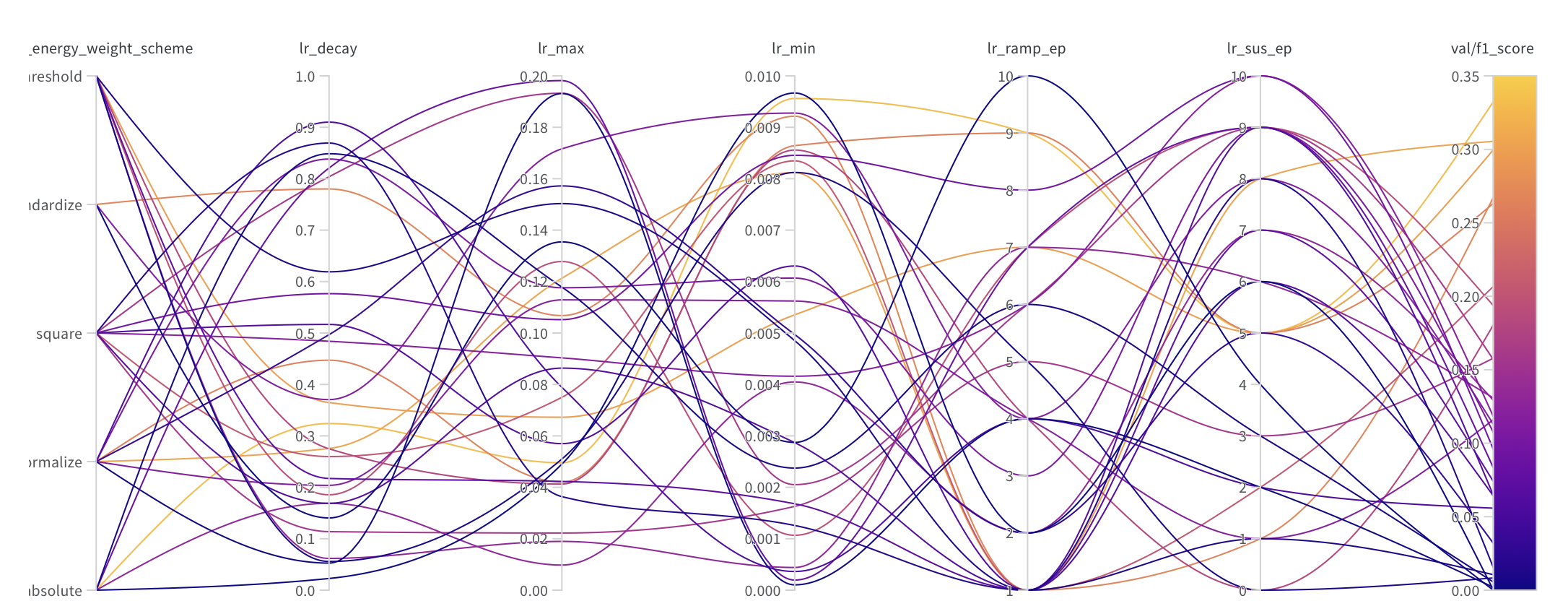
Choix d’une Métrique de Validation

L’entraînement du modèle utilise deux métriques. Tout d’abord, la fonction de perte était une fonction de perte binaire pondérée par l’entropie croisée. Cette fonction a été choisie car elle représente la relation entropique entre les valeurs prédites et réelles, ce qui est crucial pour un problème de classification, ainsi que sa différentiabilité, qui est essentielle pour la rétropropagation.

Cependant, la relation entre la fonction de perte et les performances du modèle n’est pas toujours claire, et la valeur de la fonction de perte ne se traduit pas bien en termes de confiance du réseau. Pour cette raison, au stade de la recherche des hyperparamètres, nous avons utilisé le score F1 comme métrique de validation. Les scores F1 mesurent la capacité du modèle à identifier correctement les événements de signal et de bruit. En particulier, le score F1 est la moyenne harmonique de la précision et du rappel du modèle. Le score F1 est une bonne métrique pour ce modèle car il mesure la capacité du modèle à identifier correctement les événements de signal et de bruit, ce qui est l’objectif principal du modèle. La raison pour laquelle il n’est pas utilisé comme fonction de perte est qu’il n’est pas différentiable et donc pas adapté à la rétropropagation.

Résultats

Le modèle est toujours en développement et est entraîné sur des données Monte Carlo, donc